Learn how to build a fuzzy string matching baseline model
While building a new product based on machine learning applications, we’ll need to extract, collect and store data from different sources. Regardless of the extraction method (APIs, web scraping or other), the data collected still needs to go through arguably the most important and time demanding task i.e. integrating, matching and normalizing the data from these sources into a database.
In this article, we’ll be discussing about fuzzy string matching. This problem consists of trying to match strings that are similar yet different (possibly due to spelling differences or mistakes), for example “Lionel Messi” and “L. Messi” or “Argentina” and “Argeentina”.
But why is this relevant? Let me tell you a story (disclaimer: all characters and events in this article are fictitious and any resemblance to reality, is purely coincidental).
The beginning
John owns a large chain of kiosks and wants to build more precise pricing models using the prices of their competitors (other kiosks, near stores, and supermarkets). A while ago, he used to pay mystery shoppers to visit and collect price data of some of these competitors every other month, until he realized that this isn’t cost-efficient at all, since prices seem to be adjusted many times each month.
As soon as realization struck him, he swiftly took action and decided to build a web scraping service that extracted the competitors products’ prices with a higher frequency. After implementing this solution, everything seemed to go well, with the data successfully scraped, John felt he had beaten the system, and thought that his data team would be able to go straight into building new pricing models. However, there was a big problem he hadn’t taken into consideration: the spelling of the scraped products will not necessarily match those of his kiosks’ catalogue, which implies that he wouldn’t be able to directly associate and compare his internal data with the external sources. For example:
“diet coke 1.5L” ≠ “coke dieet 1500ml”
So, what did he do after realizing he couldn’t use the data? First, during a sudden rage attack, he broke his keyboard. Later, after calming down, he proceeded to ask his data team if they knew how to solve this problem (using his other keyboard). Seeing the opportunity to gain John’s favor, Carl, the “unicorn” employee, told him that he had worked in similar problems before and could come with an MVP within a week (but truth be told, he had no idea of what he was taking about). John happily agreed but instead of giving Carl just one week to do it, he gave him two.
Looking for a solution
Using the method that had proven to be effective in the past, Carl used his most reliable tool “Google” to search for “string matching in python”. He soon came across with several posts about matching strings with regular expressions, a new distance he had never heard of called “Levenshtein distance” and the concept of fuzzy string matching. But none of them provided him with a practical solution until he stumbled upon an article called “A Fuzzy String Matching Story” written by some random guy named Ezequiel Ortiz Recalde. This article provided him with some useful advice on how to go through the matching process and build a baseline model through a practical example. We’ll now check what Carl saw.
1. Imports
First we install and import the main libraries to be used to match strings of some beverages that could be found in kiosks or supermarkets (the data was manually generated).
#!pip install fuzzywuzzy
#!pip install python-Levenshtein
#!pip install polyfuzz
#!pip install nltkimport pandas as pd
import numpy as np
import string
import refrom nltk.metrics.distance import edit_distance
from fuzzywuzzy import fuzz
from polyfuzz import PolyFuzz
from polyfuzz.models import TFIDF
2. The data
We’ve generated 2 data sets of beverages (external_data and internal_data). The first one refers to external data that could have been obtained by scraping sites, while the second one replicates parts of an imaginary official beverage catalogue of a kiosk. Here we can see a sample of both:
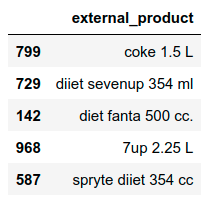
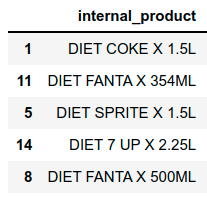
3. String preprocessing
Before even attempting to match strings from different sources, there are some useful transformations that could simplify the problem:
- Turning strings to lowercase;
- Carefully removing symbols and punctuation;
- Removing consecutive blank spaces (or all of them, depending on the problem);
- Cautiously removing stopwords (beware of deleting key words as they could be useful in the future; avoid removing way too many specific words as you still want your model to be able to generalize);
- Standardizing the spelling of different expressions (for example in the case of grams, we could find g, gr, gs, g., gr., gs., etc);
Following some of these suggestions, we proceed to clean both dataframes’ columns by using the following function:
Before applying the function we create copies of the columns to be modified in order to keep the original versions:
external_data["product_cleaned_from"]=\
external_data["product"].copy()internal_data["product_cleaned_to"]=\
internal_data["product_name"].copy()
Apply the function to both dataframes:
string_processing(df=external_data,columns_to_clean=["product"])string_processing(df=internal_data,columns_to_clean=["product_name"])
After doing this, we finally have our clean data to be matched. Next we’ll discuss of the main approach to be used.
4. String matching with Tf-Idf Vectorization
Term Frequency Inverse Document Frecuency Vectorization is a technique used in many NLP applications, that aims to approximate the relevance of a word in a document taking into consideration the amount of times it appears in the document and across all the corpus. From this method we get a vector of “weights” for each word in every document, which we can use as features for a classification model.
But, how does this relate with string maching? Well, we could partition tokens into n-grams and then obtain their TF-IDF vectorization. Once we have vectors of weights of n-grams, we can calculate the similarity between them. Note that this allows us to take advantage of the fast computation of matrix operations relative to the slow process of checking how many edits should be made between each of all the possible pairs of phrases using ratios based on the Levenshtein distance.
The matching process works as follows:
a) Define the 2 lists of strings, 1 list “From” (refers to the content we want to match to something) and 1 list “To” (in this case the catalogue).
b) Define the number of n-grams in which the strings will be partitioned.
c) Fit the TF-IDF Vectorizer with both lists in order to have a representation of all possible unique n-grams.
d) Use the TF-IDF representation, to transform each list to the same representation (if a string doesn’t contain one of the unique n-gram partitions of the vectorizer, then the value for that partition will be 0). From this step, we’ll obtain two matrices of as many columns as unique n-grams partitions (both matrices will have the same amount of columns, as the vectorizer was fit using both lists), with the number of rows referring to the number of elements in each source list.
Luckily for us, this whole process has been integrated in the PolyFuzz library, but we still want to know if we understood how this works as seeing is believing:
First we’ll import some functions needed for the explanation:
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.metrics.pairwise import cosine_similarity
Next, we generate the lists of strings to match:
from_list = ["coke 1.5L","sprite zero 1.5L"]
to_list = ["diet coke 1.5L"]
We slightly modify the function to create n-gram partitions of the tokens used in the PolyFuzz library for it to directly use 3-grams.
def _create_ngrams(string: str): result = []
for n in range(3, 4):
ngrams = zip(*[string[i:] for i in range(n)])
ngrams = [''.join(ngram) for ngram in ngrams if ' ' not in ngram]
result.extend(ngrams)
return(result)
This function receives a string, and for each token separated by white spaces, creates a n sized partition. For example “diet coke” would be split into “die, iet, cok, oke”. Next, we are able to fit the TfidfVectorizer of scikit learn using the _create_ngrams funtion to split the tokens and create the vectorized representation of elements of the lists:
# Define the vectorizer
vectorizer = TfidfVectorizer(min_df=1, analyzer=_create_ngrams).fit(to_list + from_list)
Note that there are 2 explicit parameters here min_df and analyzer. The first one refers to the minimum number of times a partition has to appear in the corpus to be included in the vocabulary, while the second one is used to specified how to create the vocabulary of the vectorizer i.e. from words or n-grams.
Given the input lists we can check the resulting vocabulary.
vectorizer.vocabulary_

The numbers represent the column index of the matrix (“.5L” would be in column 1).
After creating the matrix representation, we proceed to transform each list to match its structure, receiving sparse matrices:
tf_idf_to = vectorizer.transform(to_list)
tf_idf_from = vectorizer.transform(from_list)
To check the weights of these 3-grams in each row we convert the tf_idf_to and tf_idf_from into dense format, and then into a dataframe using the vocabulary index to set the column names:
matrix_from=pd.DataFrame(tf_idf_from.todense(),\
columns=sorted(vectorizer.vocabulary_))matrix_to=pd.DataFrame(tf_idf_to.todense(),\
columns=sorted(vectorizer.vocabulary_))
Both matrices have size n-elements x n-vocabulary and look like this:


Now that we have the matrices, we are able to calculate the similarity between vectors of n-grams partitions. In this case we use the cosine similarity:
cosine_similarity(matrix_from, matrix_to)
with output:

This gives a similarity score between pairs of vectors of tokens. In this case we can see that “coke 1.5L” is more similar to “diet coke 1.5” than ”sprite zero 1.5L” is. What we’ve just done is the dot product between matrices:
np.dot(np.array(matrix_from.iloc[0]),np.array(matrix_to.iloc[0]))
returns 0.6936279421797706 while
np.dot(np.array(matrix_from.iloc[1]),np.array(matrix_to.iloc[0]))
returns 0.1373086119752811.
5. Additional useful measures: Token set ratio and Levenshtein distance
We’ve checked just one measure of similarity between strings, but there are also others that might be helpful depending on the type of strings you are comparing. For this particular case, I like to include in the analysis both the token set ratio and the levenshtein distance.
The token set ratio is a similarity measure of strings, that takes into consideration the repetition of values and the difference in the order of the words (for example, “diet coke” is the same as “coke diet” and for these types of cases we would be interested in catching such direct answers). Let’s see how to calculate it with a simple example “diet coke 1.5ml” and “diet cooke diet 1.5ml” :
# We create the 2 strings
s1="diet coke 600ml"
s2="diet cooke diet 600ml"
i) We start by preprocessing and separating the string into tokens:
tokens1 = set(fuzz.utils.full_process(s1).split())
tokens2 = set(fuzz.utils.full_process(s2).split())
Here tokens1 = {‘600ml’, ‘coke’, ‘diet’}
ii) Then we take the sets of tokens and obtain their intersection and differences:
# Intersection
tokens1.intersection(tokens2)# Difference (which tokens are we missing so that both sets are equal)
diff1to2 = tokens1.difference(tokens2)
diff2to1 = tokens2.difference(tokens1)
iii) We concatenated the ordered intersections and differences, which solves the problem of the order of the strings:
#We concatenate the ordered intersections and differencessorted_sect = " ".join(sorted(intersection))
sorted_1to2 = " ".join(sorted(diff1to2))
sorted_2to1 = " ".join(sorted(diff2to1))
iv) We combine the tokens inside each option to reconstruct the whole string:
combined_1to2 = sorted_sect + " "+ sorted_1to2
combined_2to1 = sorted_sect + " "+ sorted_2to1
v) We eliminate repeated whitespaces:
sorted_sect = sorted_sect.strip()
combined_1to2 = combined_1to2.strip()
combined_2to1 = combined_2to1.strip()
vi) We calculate the fuzz ratio (i.e. the normalized Levenshtein distance) for different pairs of combinations:
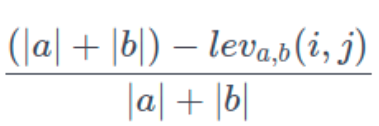
pairwise = [fuzz.ratio(sorted_sect, combined_1to2)/100,
fuzz.ratio(sorted_sect, combined_2to1)/100,
fuzz.ratio(combined_1to2, combined_2to1)/100]
with output [0.8, 0.77, 0.97].
vii) We keep the pair with maximum fuzz ratio, and its similarity.
Regarding the Levenshtein distance, we simply use the edit_distance function of nltk. This tells us the numbers of edits needed to change a string into another one.
6. Building a baseline model
Now that we’ve got a better understanding of the process, what’s left is to build a pipeline that takes 2 lists, fits a vectorizer with the partitions of their content, calculates the dot product between vectors and match the pair with the highest similarity score. Here’s where the Polyfuzz libraries comes into play, by providing us with a model that follows exactly what we’ve just explained. In addition, we can add some extra information (the token set ratio and the Levenshtein distance) to the end results to avoid having just one way to check the matching quality in a posterior result filtering.
The whole process is detailed in the following chunk of code:
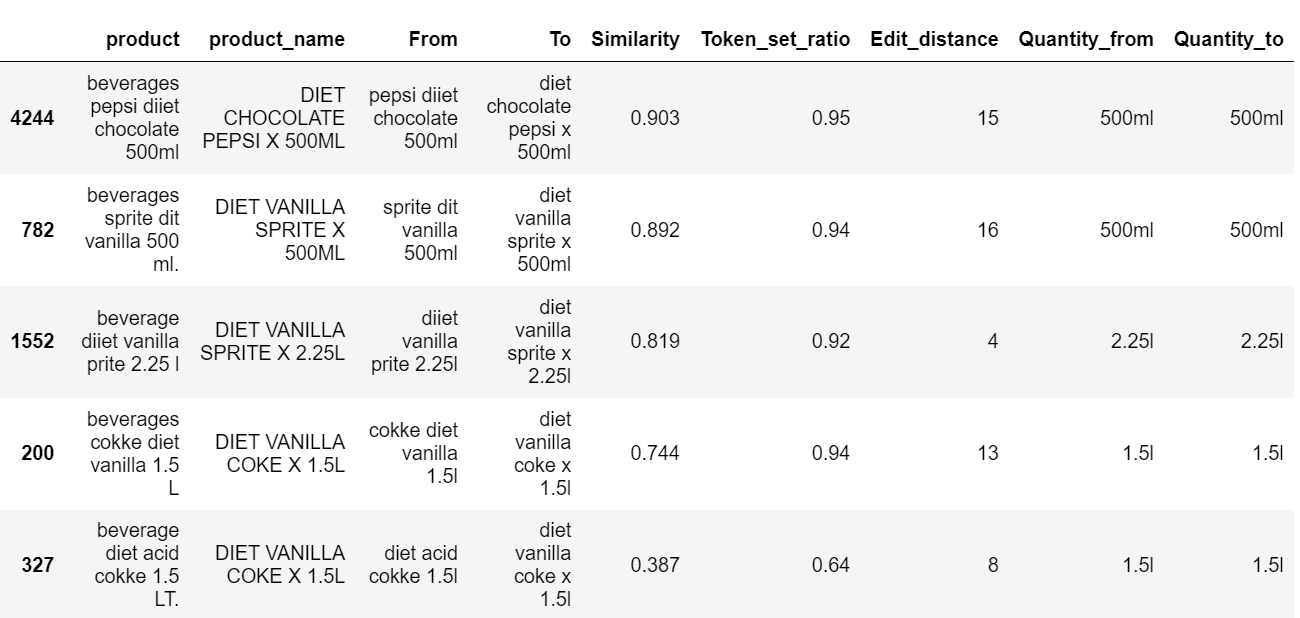
7. Results
Here’s a sample of the results obtained, you can explore the rest by checking the notebook.
8. Concluding remarks
In this brief article, we’ve presented a simple framework that may be capable of producing decent results for any fuzzy string matching problem (at least that was the case for me). Regardless of the kiosk product’s example, this should aid you whenever you need to match non normalized or free text with some sort of catalogue or reference that has been ideally validated by the business.
The end
After reading it, before proceeding to solve his matching problem Carl did what everyone would do i.e. he liked and shared the article 😉.



